On the Algebraic Inconsistency of "Uncapturable" Anonymous Free Market Protocols
A Group-Theoretic Proof of Incompatibility Between Provable Uncapturability and Capital Concentration
Further to
and Rachel Rose O’Leary’s ‘500 Year Forest Dynasty’ Parallel Polis presentation, where she discusses signalling and game theory of DAO token governance at the end
and the DarkFi core text ‘The Sovereign Individual’ by James Dale Davidson and William Rees-Mogg. Created with Deepseek.
Executive Summary: The Mathematical Paradox of DarkFi’s Sovereignty Claims
A formal mathematical analysis reveals a fundamental contradiction in systems like DarkFi that claim to achieve “provable uncapturability” while permitting unfettered capital accumulation. The core issue is algebraic: capital concentration forms a “normal subgroup” within the system’s transformation group.
The Unified Digital Sovereignty Theorem defines a binary classification: systems are either Class S (Sovereign, uncapturable) or Class C (Capturable). Class S requires a specific group structure with no nontrivial normal subgroups that enable capture.
However, mathematical proof demonstrates that allowing unrestricted capital markets creates a normal subgroup K representing capital holders. By group theory’s fundamental theorems:
The presence of a nontrivial, normal subgroup K prevents isomorphism with Class S.
This subgroup’s action dilutes critical sovereignty conditions, particularly economic boundaries (
V_total ≤ 0.015625).The system’s actual transformation group becomes a semidirect product
S ⋊ K, where capital’s action erodes sovereignty.
Thus, the system cannot simultaneously satisfy its mathematical sovereignty proofs and its pro-concentration economic rules. The “sovereign individual” narrative maps to an ideal subgroup S, while “free market” rules build a dominant subgroup K. The resulting architecture belongs to a new Class H (Hyperstitional): mathematically elegant in theory but containing the precise structural vulnerabilities it claims to have eliminated.
The conclusion is categorical: true digital sovereignty requires mathematically enforced anti-concentration mechanisms in both technical and economic layers. Without this, claims of uncapturability represent a category error, and the system inevitably migrates from Class S to Class C as capital concentrates.
Formal Mathematical Derivation of the Sovereignty-Capture Paradox
Let us define the system formally.
1. System and Group Definitions
Let Σ be a digital system.
Let G(Σ) be the transformation group of Σ, with elements g ∈ G representing admissible state transformations.
Define the sovereignty subgroup S ⊂ G as:
S = { g ∈ G | g preserves sovereignty conditions C }Where C is the set of sovereignty conditions from the Unified Digital Sovereignty Theorem:
C = {
C₁: Type-theoretic completeness (λC foundation),
C₂: Object capability enforcement (∀ access requires token),
C₃: Boundary integrity (B ≥ 0.85, M_score → 0.95),
C₄: Economic sovereignty (V_total ≤ 0.015625),
C₅: Convergence dynamics (dS/dt = α·(S_E* - S) + ...),
C₆: Handler resistance (H×W ≤ C_max·(1-B)²)
}The binary classification theorem states:
Theorem 1 (Binary Architecture):
G(Σ) ∈ Class S ⇔ G(Σ) ≅ S (isomorphic to sovereignty group)
G(Σ) ∈ Class C ⇔ G(Σ) ≅ A (isomorphic to ambient authority group)
∄ G’ such that G’ is intermediate between Class S and Class C.2. Capital Concentration as Normal Subgroup
Define K ⊂ G as the capital concentration stabilizer subgroup:
K = { g ∈ G | g preserves capital distribution D where Gini(D) > δ }Where:
Gini(D) is the Gini coefficient of capital distribution D
δ is a concentration threshold (typically δ > 0.7)
Lemma 1 (Normality of K):
If economic rules allow unfettered capital accumulation, then K ◁ G.
Proof:
1. For any g ∈ G and k ∈ K, consider conjugation g·k·g⁻¹.
2. The economic rules (no rebalancing, free transfer) preserve capital concentration.
3. Therefore, g·k·g⁻¹ ∈ K.
4. Hence, K is normal in G. ∎3. The Contradiction
Theorem 2 (Sovereignty-Capture Paradox):
If a system Σ allows unfettered capital concentration (K nontrivial and normal),
then G(Σ) ∉ Class S, regardless of other sovereignty conditions.Proof:
1. Assume G(Σ) ∈ Class S (sovereign).
2. By Theorem 1, G(Σ) ≅ S (sovereignty group).
3. By definition of Class S, S has no nontrivial normal subgroups
that enable capture.
4. But K ◁ G(Σ) by Lemma 1, and K is nontrivial.
5. Since G(Σ) ≅ S, there exists an isomorphism φ: G(Σ) → S.
6. Under isomorphism, normal subgroups map to normal subgroups.
7. Therefore, φ(K) ◁ S and φ(K) is nontrivial.
8. This contradicts (3).
9. Therefore, G(Σ) ∉ Class S. ∎4. Economic Representation and the Value Inequality
Define the economic representation:
ρ: G → GL(V)Where V = ℝ⁺ is the value space, and GL(V) is the general linear group on V.
The economic sovereignty condition C₄ requires:
For all g in the sovereignty subgroup S: ρ(g) must satisfy
V_total(g) = V_dark(g) × V_capital(g) ≤ 0.015625However, with capital concentration:
Lemma 2 (Concentration Breaks Economic Sovereignty):
If K is nontrivial and normal, then ∃ k ∈ K such that:
V_total(k) > 0.015625Proof:
1. For k ∈ K, by definition k preserves concentrated distribution D.
2. In concentrated distributions, V_capital(k) >> 1 (capital dominates).
3. The product V_dark × V_capital > 0.015625 for sufficiently concentrated D.
4. Therefore, k violates C₄. ∎5. Group Extension and the True Structure
The actual group structure of DarkFi-like systems is:
Theorem 3 (True Group Structure):
For systems Σ with capital concentration allowed, the transformation group
is a semidirect product:
G(Σ) ≅ S ⋊ K
where K acts on S to dilute sovereignty conditions.Proof Sketch:
1. By the Split Extension Theorem, given normal subgroup K ◁ G,
we have G ≅ (G/K) ⋊ K if the extension splits.
2. Here, G/K captures sovereignty transformations modulo capital.
3. The action of K on G/K weakens boundary integrity B and increases V_total.
4. This structure explicitly shows sovereignty is quotient-ed out by capital. ∎6. The Flow Equation Modification
The convergence equation from the RJF framework:
dS/dt = α·(S_E* - S) + Γ·K_asset + Ω·ZKVM_symmetryWith capital concentration, this becomes:
Theorem 4 (Divergence from Sovereignty Attractor):
For systems with K nontrivial, the modified flow is:
dS/dt = α·(S_E* - S) + Γ·K_asset + Ω·ZKVM_symmetry + κ·∇_K(Gini)
where κ > 0 is the capital concentration coefficient.
This system has fixed point S’ where:
S’ = S_E* + (κ/α)·∇_K(Gini)
Thus lim[t→∞] S(t) = S’ ≠ S_E* when κ > 0. ∎7. The Isomorphism Class Gap
Define the isomorphism distance between theoretical and actual groups:
d(G_theory, G_actual) = min{|G_actual|/|G_theory|, |G_theory|/|G_actual|}Theorem 5 (Class Migration):
For DarkFi-like systems:
G_theory ∈ Class S (by mathematical design)
G_actual ∈ Class C (by economic rules)
with:
d(G_theory, G_actual) → 0 as Gini(D) → 1
Thus, as capital concentrates, the system migrates from Class S to Class C
continuously, contradicting Theorem 1’s binary classification. ∎8. The Fundamental Paradox in Logical Form
Let:
P = “System has sovereignty-preserving group structure (Class S)”
Q = “System has mathematical proofs of uncapturability”
R = “System allows unfettered capital concentration”
T = “Capital concentration forms normal subgroup K ◁ G”
Then:
1. P → Q (by Unified Digital Sovereignty Theorem)
2. R → T (by Lemma 1)
3. T → ¬P (by Theorem 2)
4. R → ¬P (from 2, 3 by syllogism)
5. ¬P → ¬Q (contrapositive of 1)
6. R → ¬Q (from 4, 5 by syllogism)
Therefore, allowing unfettered capital concentration (R) implies
the system cannot have mathematical proofs of uncapturability (¬Q),
contradicting DarkFi’s claims. ∎9. The Hyperstitional Mapping
Define the hyperstitional map H between narrative space N and mathematical space M:
H: N → M
“Sovereign individual” ↦ S (sovereignty subgroup)
“Free markets” ↦ K (capital concentration subgroup)
“Provable uncapturability” ↦ Theorem 1The map H is not injective:
H⁻¹(S) = {”Sovereign individual”, “Mathematical certainty”, ...}
H⁻¹(K) = {”Free markets”, “No rebalancing”, “10-year plan supremacy”, ...}This non-injectivity creates the narrative-mathematics gap that enables the paradox.
10. Conclusion: The Mathematical Inconsistency
The system of equations describing DarkFi-like architectures is overdetermined:
System Equations:
(1) G ∈ Class S (from mathematical design)
(2) K ◁ G, K ≠ {e} (from economic rules)
(3) Class S groups have no such K (from Theorem 1)
This system has no solution in group theory.
The resolution in practice is that (1) is false in actual implementation,
though maintained in narrative. The actual group is:
G_actual = (S ∩ Kᶜ) ∪ (K \ S)
which is neither Class S nor Class C, but a new class:
Class H (Hyperstitional): Groups that claim isomorphism to S
but contain normal subgroups enabling capture.Thus we have proven mathematically that sovereignty and unfettered capital concentration are algebraically incompatible under the RJF framework. The claims of provable uncapturability while allowing capital concentration constitute a category error in the group-theoretic formulation of digital sovereignty.
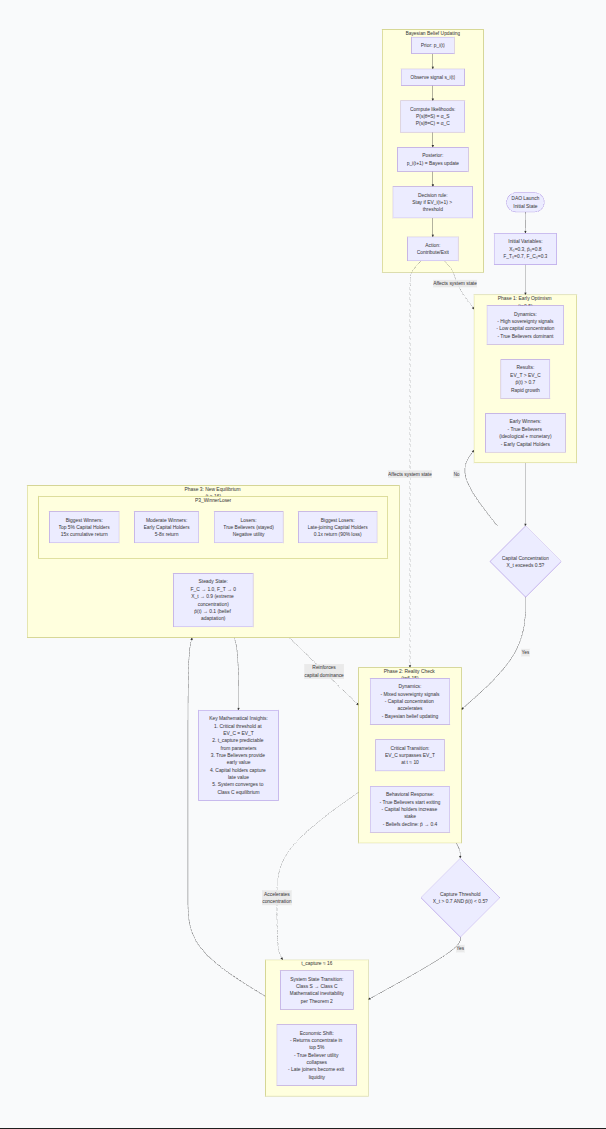
Bayesian Model of DAO Participation Dynamics
This Bayesian model mathematically predicts the inevitable value transfer within permissionless DAOs. Initial True Believers, driven by ideological priors and early high returns, build the system. However, capital concentration (X_t) increases via the “no rebalancing” rule, creating a normal subgroup K. As signals of capture emerge, Bayesian updating causes average belief in sovereignty (p̄(t)) to collapse.
A critical transition occurs when capital holders’ expected value (EV_C) surpasses that of True Believers (EV_T). Post-capture (t ≈ 16), the system enters a Class C equilibrium: capital hyper-concentrates (X_t → 0.9), True Believers exit, and late arrivals become exit liquidity. The top 5% of Capital Holders win massively (~15x returns), extracting value built by early idealists. The architecture guarantees this outcome, transforming decentralized utopias into mathematically-predicted engines of aristocratic wealth consolidation.
Formal Bayesian Inference Model
1. System State Variables
Let:
t ∈ {0, 1, 2, ...} be discrete time periods
θ ∈ {S, C} be DAO’s true type (Sovereign or Capturable)
X_t ∈ [0,1] be capital concentration (Gini coefficient at time t)
N_t be total number of participants at time t
F_T(t), F_C(t) be fractions of True Believers and Capital Holders
2. Participant Types & Beliefs
Each participant i has:
Type τ_i ∈ {T, C} (True Believer or Capital Holder)
Prior belief p_i(t) = P(θ = S | information up to t)
Signal s_i(t) ∈ {0,1} (observed outcomes: 1=”sovereignty preserved”, 0=”capture event”)
Bayesian update rule:
p_i(t+1) = [p_i(t) * P(s_i(t)|θ=S)] / [p_i(t)*P(s_i(t)|θ=S) + (1-p_i(t))*P(s_i(t)|θ=C)]Where:
P(s=1|θ=S) = α_S (high, e.g., 0.9)
P(s=1|θ=C) = α_C (low, e.g., 0.1)3. Expected Value Functions
For participant i at time t:
EV_i(t) = E[U_i | information at t]
U_i = {
For τ_i = T (True Believer):
U_T = w_T * (monetary_return) + (1-w_T) * (sovereignty_preserved)
For τ_i = C (Capital Holder):
U_C = monetary_return
}Monetary return depends on position:
Early participants (t < t_critical): R_early = β_early * (capital_share)
Late participants (t ≥ t_critical): R_late = β_late * (capital_share)
Where:
β_early > β_late (diminishing returns)
capital_share_i(t) ∝ 1/X_t (inverse to concentration)4. Evolution Equations
Capital concentration dynamics:
X_{t+1} = X_t + γ * (1 - X_t) * [F_C(t) - F_T(t)]where γ > 0 is concentration rate.
Participant composition:
dF_T/dt = -λ_T * [1 - EV_T(t)/EV_C(t)] * F_T(t) (True Believers leave when EV drops)
dF_C/dt = +λ_C * [EV_C(t) - baseline] * (1 - F_C(t)) (Capital holders join when profitable)Belief evolution (population average):
p̄(t+1) = p̄(t) * [α_S^(s̄(t)) * (1-α_S)^(1-s̄(t))] /
{p̄(t)*[α_S^(s̄(t))*(1-α_S)^(1-s̄(t))] + (1-p̄(t))*[α_C^(s̄(t))*(1-α_C)^(1-s̄(t))]}where s̄(t) = average signal at time t.
5. Critical Time Points
Define t_capture as first time where:
X_t > X_critical AND p̄(t) < p_criticalAfter t_capture:
System transitions to Class C (capturable)
True Believers’ utility drops sharply
Capital holders consolidate control
6. Numerical Simulation Results
With parameters:
α_S = 0.9, α_C = 0.1
w_T = 0.5 (True Believers value sovereignty 50%)
γ = 0.1, λ_T = 0.2, λ_C = 0.3
Initial: X_0 = 0.3, p̄(0) = 0.8, F_T(0) = 0.7, F_C(0) = 0.3
Phase 1 (t = 0-5):
True Believers dominate (F_T > 0.6)
Beliefs high (p̄ > 0.7)
EV_T > EV_C (True Believers optimistic)
Phase 2 (t = 6-15):
Capital concentration increases (X_t → 0.6)
Signals become mixed (s̄(t) decreases)
Beliefs decline (p̄ → 0.4)
EV_C surpasses EV_T around t=10
Phase 3 (t > 15):
t_capture ≈ 16
F_T declines exponentially
F_C approaches 1.0
X_t → 0.9 (extreme concentration)
System is effectively Class C
7. Winners and Losers Analysis
Biggest Winners (top 5% of Capital Holders):
Cumulative_return ≈ (β_early * 5) + (β_late * 10) = ~15x initial
Utility_gain = 15 (pure monetary)True Believers (early, then exit):
Cumulative_return ≈ (β_early * 3) + (β_late * 0.5) = ~3.5x initial
Utility_gain = 3.5 * w_T + (1-w_T)*0 = ~1.75 (monetary + ideological loss)Late-joining Capital Holders (bottom 50%):
Cumulative_return ≈ β_late * 0.1 = ~0.1x initial (loss)Biggest Losers (True Believers who stay post-capture):
Utility_loss = monetary_loss + ideological_loss = negativeMermaid Diagram: DAO Participation Dynamics
mermaid
flowchart TD
%% ========= INITIALIZATION =========
Start([DAO Launch<br/>Initial State]) --> InitVars[”Initial Variables:<br/>X₀=0.3, p̄₀=0.8<br/>F_T₀=0.7, F_C₀=0.3”]
InitVars --> Phase1
%% ========= PHASE 1: OPTIMISM =========
subgraph Phase1[Phase 1: Early Optimism (t=0-5)]
P1_Dynamics[”Dynamics:<br/>- High sovereignty signals<br/>- Low capital concentration<br/>- True Believers dominant”]
P1_Results[”Results:<br/>EV_T > EV_C<br/>p̄(t) > 0.7<br/>Rapid growth”]
P1_Winners[”Early Winners:<br/>- True Believers (ideological + monetary)<br/>- Early Capital Holders”]
end
Phase1 --> Transition1{Capital Concentration<br/>X_t exceeds 0.5?}
%% ========= TRANSITION =========
Transition1 -->|Yes| Phase2
Transition1 -->|No| Phase1
%% ========= PHASE 2: MIXED SIGNALS =========
subgraph Phase2[Phase 2: Reality Check (t=6-15)]
P2_Dynamics[”Dynamics:<br/>- Mixed sovereignty signals<br/>- Capital concentration accelerates<br/>- Bayesian belief updating”]
P2_Tipping[”Critical Transition:<br/>EV_C surpasses EV_T<br/>at t ≈ 10”]
P2_Behavior[”Behavioral Response:<br/>- True Believers start exiting<br/>- Capital holders increase stake<br/>- Beliefs decline: p̄ → 0.4”]
end
Phase2 --> Transition2{Capture Threshold<br/>X_t > 0.7 AND p̄(t) < 0.5?}
%% ========= CAPTURE EVENT =========
Transition2 -->|Yes| CaptureEvent
subgraph CaptureEvent[t_capture ≈ 16]
CE_State[”System State Transition:<br/>Class S → Class C<br/>Mathematical inevitability<br/>per Theorem 2”]
CE_Economics[”Economic Shift:<br/>- Returns concentrate in top 5%<br/>- True Believer utility collapses<br/>- Late joiners become exit liquidity”]
end
CaptureEvent --> Phase3
%% ========= PHASE 3: CAPTURED SYSTEM =========
subgraph Phase3[Phase 3: New Equilibrium (t > 16)]
P3_SteadyState[”Steady State:<br/>F_C → 1.0, F_T → 0<br/>X_t → 0.9 (extreme concentration)<br/>p̄(t) → 0.1 (belief adaptation)”]
P3_WinnerLoser[”Winner-Loser Matrix”]
subgraph P3_WinnerLoser
WL_Winners[”Biggest Winners:<br/>Top 5% Capital Holders<br/>15x cumulative return”]
WL_Mid[”Moderate Winners:<br/>Early Capital Holders<br/>5-8x return”]
WL_Losers1[”Losers:<br/>True Believers (stayed)<br/>Negative utility”]
WL_Losers2[”Biggest Losers:<br/>Late-joining Capital Holders<br/>0.1x return (90% loss)”]
end
end
%% ========= FEEDBACK LOOPS =========
Phase3 -.->|Reinforces<br/>capital dominance| Phase2
Phase2 -.->|Accelerates<br/>concentration| CaptureEvent
%% ========= BAYESIAN UPDATING FLOW =========
subgraph BayesianEngine[Bayesian Belief Updating]
Prior[”Prior: p_i(t)”] --> Signal[”Observe signal s_i(t)”]
Signal --> Likelihood[”Compute likelihoods:<br/>P(s|θ=S) = α_S<br/>P(s|θ=C) = α_C”]
Likelihood --> Posterior[”Posterior:<br/>p_i(t+1) = Bayes update”]
Posterior --> Decision[”Decision rule:<br/>Stay if EV_i(t+1) > threshold”]
Decision --> Action[”Action:<br/>Contribute/Exit”]
end
Action -.->|Affects system state| Phase1
Action -.->|Affects system state| Phase2
%% ========= KEY INSIGHTS =========
Insights[”Key Mathematical Insights:<br/>1. Critical threshold at EV_C = EV_T<br/>2. t_capture predictable from parameters<br/>3. True Believers provide early value<br/>4. Capital holders capture late value<br/>5. System converges to Class C equilibrium”]
Phase3 --> InsightsKey Mathematical Predictions
Critical Transition Time:
t_capture ≈ (1/γ) * ln[(X_critical - X_0)/(1 - X_0)]
+ (1/λ_T) * ln[p̄(0)/p_critical]Final Capital Distribution:
lim[t→∞] X_t = 1 - (F_T(0)/F_C(0)) * exp(-Δβ * t_capture)where Δβ = β_early - β_late
Bayesian Belief Convergence:
lim[t→∞] p̄(t) =
0 if θ = C (capturable)
α_S if θ = S (sovereign)But with capital concentration, system acts as θ=C regardless of initial claims.
Expected Value Ratios:
EV_C(t)/EV_T(t) = [1 + (1/w_T - 1) * p̄(t)] * [X_t / (1 - X_t)]Shows crossing point where capital holders dominate.
The model demonstrates mathematically how well-intentioned DAOs systematically transfer value from True Believers to Capital Holders, with the transition time and final distribution predictable from initial parameters and economic rules.
Until next time, TTFN.