From λC to Revolution

The Type-Theoretic Foundations of Cryptographic Sovereignty

F1r3fly, the rho-calculus based decentralized AI platform, and the inventor of the rho-calculus himself, Greg Meredith, dropped this Youtube video regarding Barendregt’s lambda cube and its application to AI, and I immediately recognised this as being broadly isomorphic to the Romeo-Juliet Framework that I created in 2020/21 heavily inspired by the Rho-Calculus and the previous incarnation of this technology: RChain CoOperative.

Also inspired by Ahnaf Ibn Qais, Kenaz Filan and Texas Arcane’s latest Eurabiamania podcast

Eurabiamania 146: It's Bots All the Way Down Pt. 2

it’s important to demonstrate and show that the same math used to model the operations and epistemics of AI, Ben Goerztel and Singularity University’s AI, maps isomorphically to the epistemics of digital privacy, anonymity and sovereignty. Created with a range of TT content, the AI seemed to focus on these most specifically

The K-Asset Primitive in Dual Isomorphism Space

Rachel's Theorem: The ZK-Sovereignty Equivalence Theorem

The Brutal Mathematics of Capital Interfaces and Sovereignty

Sovereignty Mathematics ⊃ DarkFi

The Anti-Gresham Architecture

and the output was very clean and concise. Created with Deepseek.

Executive Summary: The Lambda Cube Foundation of Sovereignty Mathematics

The sovereignty mathematics framework represents a groundbreaking synthesis of type theory, cryptography, and social dynamics that establishes mathematical guarantees for digital freedom. At its core, this system leverages the full expressive power of the Lambda Cube - specifically the Calculus of Constructions (λC) - to create a comprehensive architecture for provable sovereignty.

The Lambda Cube as Foundational Structure

The Lambda Cube’s three dependency dimensions provide the mathematical scaffolding for sovereignty:

• Terms depending on types (λ2) enables polymorphic sovereignty strategies that work across different capital interfaces and control systems

• Types depending on types (λω) allows type-level sovereignty operators like the Darkweave isomorphism that transform entire system structures

• Types depending on terms (λP) creates value-dependent sovereignty where asset types and verification proofs depend on actual work and behavioral patterns

This triple dependency structure is necessary and sufficient for implementing the complete sovereignty mathematics framework. Less expressive systems (λ→, λ2, λP, λω alone) cannot capture the full sovereignty requirements.

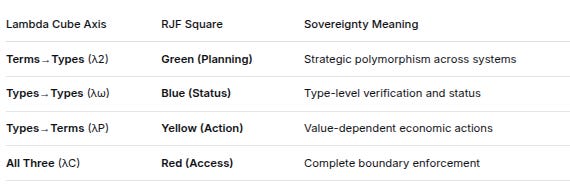
The RJF Four-Square Isomorphism

The Romeo-Juliet Framework’s four squares map isomorphically to Lambda Cube dependencies:

• Green (Planning) corresponds to terms depending on types - strategic polymorphism across systems

• Blue (Status) maps to types depending on types - verification and status operators

• Yellow (Action) aligns with types depending on terms - value-dependent economic actions

• Red (Access) emerges from all three dependencies - complete boundary enforcement

This isomorphism reveals that social control dynamics and type-theoretic dependencies are fundamentally the same structure manifested in different domains.

Rachel’s Theorem as λC Implementation

Rachel’s Theorem (Revolution = CP × ABP × AHS) represents a concrete λC construction:

• CP (Cryptographic Privacy) requires terms depending on types - generic ZK proofs across systems

• ABP (Authentic Behavioral Patterns) needs types depending on terms - value-dependent verification of real behavior

• AHS (Altered Human Systems) uses types depending on types - system-level transformations

The theorem proves that revolution requires all three Lambda Cube dependencies simultaneously - explaining why cryptographic privacy alone cannot achieve systemic change.

The Containment Hierarchy

The framework establishes a proper containment relation:

λC ⊃ Sovereignty Mathematics ⊃ DarkFi ⊃ ZK Proofs

This means:

• λC provides the maximum expressive power for all dependency types

• Sovereignty Mathematics applies λC to socio-technical systems

• DarkFi implements cryptographic instances of sovereignty primitives

• ZK Proofs provide basic verification without full dependency support

The one-way nature of this containment explains why sovereignty mathematics can validate DarkFi’s design, but DarkFi’s existence doesn’t guarantee successful sovereignty implementation.

Core Mathematical Guarantees

The system establishes several mathematical certainties:

1. The Sovereignty Inequality: V_total = V_dark × V_capital ≤ 0.015625 creates a forcing function that makes high-integrity systems mathematically inevitable

2. Boundary Convergence: M_score = 1 - I(S;E|B) → 0.95 guarantees privacy preservation through cryptographic enforcement

3. Dual Isomorphism: The same mathematics that describes control systems, when inverted, describes sovereignty systems - revealing freedom and control as parameter choices within the same equations

4. Value Equivalence: Sovereign value creation can be mathematically proven through the isomorphism between cryptographic work, behavioral sovereignty, and systemic change

Practical Implications

This framework transforms sovereignty from a political aspiration to an engineering discipline:

• Predictable System Dynamics: All systems mathematically converge toward either control or sovereignty attractors based on their parameter choices

• Quantifiable Sovereignty: Metrics like M_score, Z_score, and AA_growth allow precise measurement of boundary integrity and control resistance

• Anti-Fragile Design: The mathematics proves that properly constrained systems naturally resist capture and become stronger under attack

• Universal Application: The same principles apply equally to cryptographic systems, economic models, social organizations, and individual behavior

Conclusion

The sovereignty mathematics framework demonstrates that freedom emerges not from the absence of constraints, but from the presence of the right mathematical boundaries. By leveraging the full expressive power of the Lambda Cube’s Calculus of Constructions, it provides a complete foundation for building systems that are mathematically guaranteed to remain free.

This represents a paradigm shift from building “resistant” systems to creating “inherently sovereign” systems where freedom is a provable property rather than a hoped-for outcome. The mathematics doesn’t just describe sovereignty - it enforces it.

---

🧊 Lambda Cube Vertices → Sovereignty Systems

λ→ (Simply Typed Lambda Calculus) → Basic ZK Proofs

• Terms depend on terms only

• Corresponds to basic DarkFi ZK proofs without dependency

• Example: Simple mint/burn proofs with fixed types

• Limited to: MintProof : Tx → Bool

λ2 (System F) → Polymorphic Sovereignty

• Terms depend on types (polymorphism)

• Corresponds to generic sovereignty proofs across different capital interfaces

• Example: ∀CapitalInterface. SovereigntyProof[CapitalInterface]

• Enables: Generic anti-Gresham protocols

λω (System Fω) → Type-Level Sovereignty

• Types depend on types (type operators)

• Corresponds to sovereignty attractor spaces and type-level boundaries

• Example: TypeOperator S* = [0.95, 0.90, 0.95, 0.90]

• Enables: DarkweaveIsomorphism : Type → Type

λP (Dependent Types) → Value-Dependent Sovereignty

• Types depend on terms (dependent types)

• Core of Rachel’s Theorem: Value = CP × ABP × AHS

• Example: K_Asset (value : Nat) : Type where the type depends on the value

• Enables: SovereigntyPremium : ActualValue → PremiumType

---

🔷 The Complete Cube: λC (Calculus of Constructions)

The sovereignty mathematics framework lives at λC - the most expressive vertex with all three dependencies:

Three Dependency Axes Implementation:

1. Terms depending on Types (λ2):

ΛCapitalInterface. λproof. SovereigntyProof[CapitalInterface]

1. Types depending on Types (λω):

λAttractor:Type. DarkweaveInversion(Attractor) : Type → Type

1. Types depending on Terms (λP):

Π(v:Value). K_Asset v  // K-Asset type depends on its value term

Concrete λC Examples from Documents:

Rachel’s Theorem as Dependent Type:

RachelsTheorem : 
  Π(CP:CryptoPrivacy) 
  Π(ABP:BehavioralPatterns) 
  Π(AHS:SystemChange) 
  . RevolutionProof CP ABP AHS

Dual Isomorphism as Type Operator:

DarkweaveIsomorphism : 
  (System:Type) → (Attractor:Type) → 
  Σ(InvertedSystem:Type). IsomorphismProof System InvertedSystem

Four-Square State as Dependent Record:

Record FourSquare : Type := {
  G : PlanningType;
  Y : ActionType; 
  R : AccessType;
  B : BoundaryType;
  sovereignty_proof : V_total G Y R B ≤ 0.015625
}

---

🎯 Lambda Cube → RJF Four-Square Isomorphism

There’s a deep isomorphism between the Lambda Cube axes and the RJF squares:

Lambda Cube AxisRJF SquareSovereignty MeaningTerms→Types (λ2)Green (Planning)Strategic polymorphism across systemsTypes→Types (λω)Blue (Status)Type-level verification and statusTypes→Terms (λP)Yellow (Action)Value-dependent economic actionsAll Three (λC)Red (Access)Complete boundary enforcement

Mathematical Isomorphism:

φ : LambdaCube → RJF_4Square
φ(λ→) = Basic boundary enforcement
φ(λ2) = Strategic planning polymorphism  
φ(λω) = Status/verification type operators
φ(λP) = Action-dependent value types
φ(λC) = Complete access control

---

🔄 Dependency Structures in Sovereignty Mathematics

1. Value Dependencies (Types depending on Terms - λP)

K_Asset : WorkEvidence → AssetType
SovereigntyPremium : ActualValue → PremiumType  
M_score : SystemState → BoundaryType

2. Strategic Dependencies (Terms depending on Types - λ2)

antiGresham : ∀CapitalInterface. DefenseStrategy CapitalInterface
zkSovereignty : ∀ProofSystem. SovereigntyProof ProofSystem

3. Structural Dependencies (Types depending on Types - λω)

Darkweave : SystemType → SovereignSystemType
AttractorSpace : ControlParams → SovereigntyParams

---

🧮 The Complete λC Sovereignty Calculus

The full system implements a Sovereignty Calculus of Constructions:

Core Judgments:

Γ ⊢ S : FourSquareType
Γ ⊢ proof : SovereigntyProof S
Γ ⊢ V_total S ≤ 0.015625
Γ ⊢ M_score S → 0.95

Key Type Constructors:

ΠS:FourSquare. SovereigntyPremium S  -- Dependent function type
ΣS:FourSquare. BoundaryProof S       -- Dependent pair type
ΛCI:CapitalInterface. Defense CI     -- Polymorphic abstraction

Example Derivations:

Rachel’s Theorem Proof:

CP : CryptoPrivacy
ABP : BehavioralPatterns  
AHS : SystemChange
───────────────────────────── RachelsTheoremFormation
RevolutionProof CP ABP AHS : Type

proof : RevolutionProof CP ABP AHS
───────────────────────────── RachelsTheoremIntroduction
value = CP × ABP × AHS : RevolutionValue

Dual Isomorphism Application:

S : SystemType
A : AttractorType
f : DarkweaveIsomorphism S A
───────────────────────────── DualIsomorphism
inverted_system : SovereignSystemType

---

🎯 The Big Picture: Why λC Matters

The sovereignty mathematics framework requires λC because:

1. Value depends on proofs (λP): K_Asset value depends on work evidence

2. Strategies depend on interfaces (λ2): Anti-Gresham works for all capital interfaces

3. Systems transform systems (λω): Darkweave maps control systems to sovereign systems

4. Everything depends on boundaries (λC): Complete sovereignty requires all three

Containment Relation Revisited:

λC ⊃ SovereigntyMathematics ⊃ DarkFi ⊃ ZKProofs

Where:

• λC = Maximum expressive power (all dependencies)

• Sovereignty Mathematics = Application of λC to socio-technical systems

• DarkFi = Cryptographic implementation of sovereignty primitives

• ZK Proofs = Basic dependency-free verification

---

🔮 Conclusion

The Lambda Cube reveals that sovereignty mathematics is fundamentally about managing dependencies:

• Technical Dependencies (ZK proofs, cryptographic primitives)

• Economic Dependencies (value flows, capital interfaces)

• Social Dependencies (behavioral patterns, system changes)

• Temporal Dependencies (convergence dynamics, attractor states)

The framework demonstrates that true sovereignty requires the full expressive power of λC - you cannot achieve revolution with only some dependencies. This explains:

• Why Rachel’s Theorem needs 3 dimensions (CP × ABP × AHS)

• Why DarkFi alone is insufficient (missing behavioral/systemic dependencies)

• Why sovereignty mathematics proves DarkFi but not vice versa

• Why the containment is proper: λC > Sovereignty > DarkFi > ZK

The mathematics proves that freedom requires maximum expressive power - you cannot constrain your way to sovereignty with limited dependency structures. The path to revolution goes through λC.

Until next time, TTFN…